If we assume that the growth in Supply and Demand is defined by Price,
whereas the decline of Supply is determined by Demand and the decline in
Demand is determined by Supply directly, we come up with a model that
produces some strange dynamics. Try to figure out what causes this strange dynamics.
What are the other possible trajectories that may be generated?
Is there an equilibrium?
It seems that delays cause the wonky behavior. Notice that as demand rises, price rises but lag behind. And as price starts to rise, supply is still falling. It looks like the slope of supply is driven by the inflection of price. That is, when the second derivative of the price function is negative, supply falls, whether price is increasing or decreasing. But I think that in the market, as price falls, regardless of its second derivative, supply would also fall.
By removing the direct informational link between supply and demand; that is, with price as their only intermediary, the behavior generated is similar to that of the predator-prey system from the chapter before last. There's no equilibrium here, because there's no mechanism for supply or demand to fall we just get continuous growth.
Wednesday, November 30, 2011
7.3 - Price/quantity model
Put together the Price - Goods model in Stella or download it from here. Try to find another function or set of parameters that would
make it converge faster.
I tweaked the parameters and production/consumption functions and to get faster convergence. I ended up with the following parameters and functions:
C_g1 = 0.02
C_g2 = 0.03
C_p1 = 0.0055
C_p2 = .06
Production = C_g1*Price^1.55
Consumption = 1/C_g2/Price^0.25
I tweaked the parameters and production/consumption functions and to get faster convergence. I ended up with the following parameters and functions:
C_g1 = 0.02
C_g2 = 0.03
C_p1 = 0.0055
C_p2 = .06
Production = C_g1*Price^1.55
Consumption = 1/C_g2/Price^0.25
 |
| Old |
 |
| New |
7.2 - Human population model with economic data
I built a new model for this exercise but kept the immigration and emigration graphical functions from the last exercise because they don't relate in any obvious way to time or prosperity. I modeled per capita GDP as a function of time: GDP = 1.826*e ^ (.02*t) where t = year with 1851 = 0. I developed that equation from a quick web search for historical economic data. I then modeled natality and mortality as functions of per capita income: natality = 0.0507*GDP^-0.34 and mortality = 0.0268*GDP^-0.377. Here is the result:
7.1 - Human Population Model
Try to improve the calibration of the population model by further modifying
the parameters a1 and
a2. You can either continue
the trial and error exercises or upload the model into Madonna and try
the curve-fitting in there. Do not forget to add the Error function to
the model since visual comparison becomes quite hard once we get really
close to the optimal solution. Is there a better combination of parameters
than a1 = a2 = 0.1?
I tried messing with the coefficients quite a bit, and I get the best performance with ain = 0.1 and aout = 0.11. The pink line is the error function, defined as 100*(Population-DATA)/Population.
I tried messing with the coefficients quite a bit, and I get the best performance with ain = 0.1 and aout = 0.11. The pink line is the error function, defined as 100*(Population-DATA)/Population.
Friday, November 4, 2011
Ex 6.6 - Global hydrological model
1. What modifications should be made to the conceptual model if a time scale
of 1 year and a spatial scale of 1 km2 are chosen for the
model? What processes can be excluded? simplified? described in more
detail?
The elevation aspect of the model can be excluded; it is important when there is flow between adjacent cells, but if we're just modeling a single area, it is irrelevant. The climatic data, on the other hand, could be made more precise, both temporally and spatially.
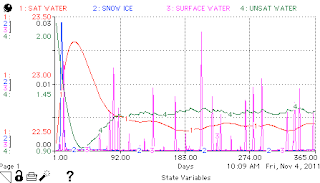
2. Compare dry year (halved precipitation) and wet year (doubled precipitation) dynamics within the model. Does the model produce reasonable estimates for the state variables? Does it tend to an equilibrium if such conditions prevail, or it shows a trend over several years?
It does reach an equilibrium, and equilibrium levels of saturated water and unsaturated water are remarkably similar despite the four-fold difference in precipitation. What does change quite significantly is the amount of surface water (and snowpack):
The same patterns and equilibria hold when the simulation is run over three years.
3. Can you find a parameter in this model, modifying which you can produce a trend over several years that destabilizes the system?
First of all, I love these how-to-break-the-system questions.
Second, if we're given sufficient latitude with the parameters, the question becomes rather simple. Increasing transpiration potential by a factor of ten does little to the system; it remains stable at a very similar equilibrium; however, increasing the same parameter by a factor of 1000 sucks all the water right out of the system:
The elevation aspect of the model can be excluded; it is important when there is flow between adjacent cells, but if we're just modeling a single area, it is irrelevant. The climatic data, on the other hand, could be made more precise, both temporally and spatially.
2. Compare dry year (halved precipitation) and wet year (doubled precipitation) dynamics within the model. Does the model produce reasonable estimates for the state variables? Does it tend to an equilibrium if such conditions prevail, or it shows a trend over several years?
It does reach an equilibrium, and equilibrium levels of saturated water and unsaturated water are remarkably similar despite the four-fold difference in precipitation. What does change quite significantly is the amount of surface water (and snowpack):
 |
| Half precipitation |
 |
| 1x precipitation |
 |
| Double precipitation |
3. Can you find a parameter in this model, modifying which you can produce a trend over several years that destabilizes the system?
First of all, I love these how-to-break-the-system questions.
Second, if we're given sufficient latitude with the parameters, the question becomes rather simple. Increasing transpiration potential by a factor of ten does little to the system; it remains stable at a very similar equilibrium; however, increasing the same parameter by a factor of 1000 sucks all the water right out of the system:
 |
| 1000-fold increasing in transpiration potential |
Thursday, November 3, 2011
Ex 6.5 - Saturated soil zone dynamics
1. Why do the dynamics of unsaturated water look so much smoother in
this model if compared to the model for
unsaturated water only?
In the unsaturated zone-only model, water that percolates out of the unsaturated zone is lost from the system. In the newer model, water that percolates out of the unsaturated zone enters the saturated zone. As a result, when precipitation falls and the site dries out, the unsaturated zone will recover water from the saturated zone, which will stabilize its levels. This wasn't possible in the older model because that water had left the system.
As evidence of this, notice that when precipitation falls, around day 200, percolation goes deeply negative and water moves from the saturated to the unsaturated zone. A miniature version of similar dynamics occurs again around day 600.
2. Can you make all the ground saturated and the unsaturated layer disappear from the system? What parameters need to be changed? What is their ecological meaning?
Is it just me or is this question, A) weird, and B) trivial?
That said, you have to check the "non-negative" boxes for both stocks, to make this happen, but that's physically legitimate -- you can't have a negative amount of ground water.
Cranking transpiration up by an order of magnitude causes both stocks to go to zero within a year:
The ecological meaning of this is that plants are pulling more water out of the unsaturated layer, from whence it evaporates through their leaves, and the unsaturated water, in turn, sucks water from the saturated water, which then also ends up moving through the plants.
In the unsaturated zone-only model, water that percolates out of the unsaturated zone is lost from the system. In the newer model, water that percolates out of the unsaturated zone enters the saturated zone. As a result, when precipitation falls and the site dries out, the unsaturated zone will recover water from the saturated zone, which will stabilize its levels. This wasn't possible in the older model because that water had left the system.
As evidence of this, notice that when precipitation falls, around day 200, percolation goes deeply negative and water moves from the saturated to the unsaturated zone. A miniature version of similar dynamics occurs again around day 600.
2. Can you make all the ground saturated and the unsaturated layer disappear from the system? What parameters need to be changed? What is their ecological meaning?
Is it just me or is this question, A) weird, and B) trivial?
That said, you have to check the "non-negative" boxes for both stocks, to make this happen, but that's physically legitimate -- you can't have a negative amount of ground water.
Cranking transpiration up by an order of magnitude causes both stocks to go to zero within a year:
The ecological meaning of this is that plants are pulling more water out of the unsaturated layer, from whence it evaporates through their leaves, and the unsaturated water, in turn, sucks water from the saturated water, which then also ends up moving through the plants.
Ex 6.4 - Unsaturated soil zone dynamics
1. What other processes are important to define the flooding regime in the area?
What paramters need to be changed to restore the drainage of the area and
make sure that it does not get flooded? What ecological processes correspond to
these changes in parameters?
There may be runoff from the site or movement of water out of the saturated zone, either of which would relieve flooding. Also, as the site gets wetter, the species composition of the vegetation of the site may change. The Gaia Principle suggests that the biota can regulate abiotic conditions to maintain them in the range that is suitable for life. Thus, as the site floods, plants with high transpiration rates may proliferate, removing water from the site in a nice feedback loop.
Finally, the amount of vegetation on the site will change with hydrological conditions. NPP stands for net primary productivity; it is the amount of carbon assimilated by an ecosystem per unit time. I have two issues with how NPP is incorporated in this model.
2. In fact when the Unsat_Depth decreases, certain amounts of unsaturated water get lost because they are no longer in the unsaturated zone. Imagine the water table rising and therefore the saturated water occupying more of the unsaturated zone. The unsaturated water in that marginal loss of the unsaturated depth will be lost from the Unsat_Water stock. Add this process to the Stella model. Is there a big difference in the results?
Wow, this question took me way too much struggle, I think because I was confused by the units in the original model. Unsat_Depth sounds to me like it should be in meters, while Unsat_Water should be in cubic meters or liters, but to keep it simple the original model is all in depth. So, all I had to do was add this conditional to the percolation statement:
This change alters the behavior of the model very little because as the system is set up, unsat_depth is almost always greater than unsat_water. With different parameter values, though, it could make quite a difference.
There may be runoff from the site or movement of water out of the saturated zone, either of which would relieve flooding. Also, as the site gets wetter, the species composition of the vegetation of the site may change. The Gaia Principle suggests that the biota can regulate abiotic conditions to maintain them in the range that is suitable for life. Thus, as the site floods, plants with high transpiration rates may proliferate, removing water from the site in a nice feedback loop.
Finally, the amount of vegetation on the site will change with hydrological conditions. NPP stands for net primary productivity; it is the amount of carbon assimilated by an ecosystem per unit time. I have two issues with how NPP is incorporated in this model.
- In the model, NPP is a defined dataset, changing only with the season, but in reality, NPP would change with the hydrological status of the site. When the site gets very dry, NPP declines. To a point, as the site moves closer to saturation, NPP increases, increasing transpiration (per the Gaia Principle), in a self-regulating feedback loop.
- A more fundamental problem is that NPP is a rate, but it is used in the model as a stock. NPP is the rate of accumulation of biomass. But in modeling transpiration as NPP * transpiration rate (on a tissue-mass basis), NPP is being confused with plant biomass. That is, transpiration should be a function of standing biomass * transpiration per unit of biomass, not biomass added per unit time * transpiration per unit of biomass.
2. In fact when the Unsat_Depth decreases, certain amounts of unsaturated water get lost because they are no longer in the unsaturated zone. Imagine the water table rising and therefore the saturated water occupying more of the unsaturated zone. The unsaturated water in that marginal loss of the unsaturated depth will be lost from the Unsat_Water stock. Add this process to the Stella model. Is there a big difference in the results?
Wow, this question took me way too much struggle, I think because I was confused by the units in the original model. Unsat_Depth sounds to me like it should be in meters, while Unsat_Water should be in cubic meters or liters, but to keep it simple the original model is all in depth. So, all I had to do was add this conditional to the percolation statement:
if Unsat_Water>Unsat_DepthOriginally I had it as a seperate outflow from unsat_water, but then you could get outflow both due to percolation and the water table rising, which would be the same water leaving twice, so that's why I put it in the percolation, despite it making a fairly long conditional.
then (Unsat_Water-Unsat_Depth)*dt
This change alters the behavior of the model very little because as the system is set up, unsat_depth is almost always greater than unsat_water. With different parameter values, though, it could make quite a difference.
Subscribe to:
Comments (Atom)





